Les nombres signés
Le codage binaire vu dans les paragraphes précédents est appelé codage binaire pur et permet de coder des nombres positifs de 0 à 2n-1.
Pour représenter des nombres signés, on pourrait rajouter un bit de signe au nombre.
Nbres positifs |
000 = 0 |
001 = 1 |
010 = 2 |
011 = 3 |
Nbres négatifs |
100 = -0 |
101 = -1 |
110 = -2 |
111 = -3 |
Cette représentation n'est pas utilisée car elle se traduit par une double représentation du 0 ce qui n'est pas pertinent.
Complément vrai ou complément à deux
Cette méthode se caractérise par :
- une seule représentation du 0
- la somme des opposés est égale à 0
- une seule valeur négative de plus que de valeur positive
- codage et décodage passe par la même méthode
 Pour obtenir le complément vrai :
Pour obtenir le complément vrai :
- inverser les états logiques du nombre N (appelé complément à 1)
- ajouter 1 au résultat
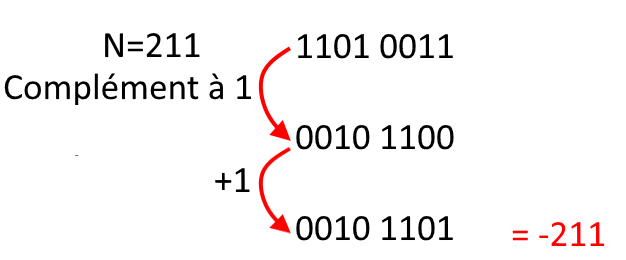
 Application 1 : 255-211 = %1111 1111 + %0010 1101 = %1 0010 1100 = %1 0010 1100
Application 1 : 255-211 = %1111 1111 + %0010 1101 = %1 0010 1100 = %1 0010 1100
Le résultat sur les 8 premiers bits donne 44. On ignore le débordement.
 Application 2 : 200-211 = %1100 1000 + %0010 1101 = %1111 0101. Pas de débordement la valeur est négative.
Application 2 : 200-211 = %1100 1000 + %0010 1101 = %1111 0101. Pas de débordement la valeur est négative.
En faisant le complément à 2 on obtient la valeur 11 soit -11